Predicting the Water Balance from Optimization of Plant Productivity

How soil-water flows and how fast it moves solutes are important for plant growth and soil formation. The relationship describing the partitioning of precipitation, P, into run-off, Q, and evapotranspiration, ET, is called the water balance. Q incorporates both surface runoff and subsurface flow components, the latter chiefly contributing to soil formation. At shorter time intervals, soil-water storage, S, may change, dS/dt, due to atmosphere-soil water exchange; i.e., infiltrating and evaporating water and root uptake. Over sufficiently long time periods, storage changes are typically neglected (Gentine et al., 2012). Percolation theory from statistical physics provides a powerful tool for predicting soil formation and plant growth (Hunt, 2017) by means of modeling soil pore space as networks, rather than continua.

In heterogeneous soils, solute migration typically exhibits non-Gaussian behavior, with statistical models having long tails in arrival time distributions and velocities decreasing over time. Theoretical prediction of solute transport via percolation theory that generates accurate full non-Gaussian arrival time distributions has become possible only recently (Hunt and Ghanbarian, 2016; Hunt and Sahimi, 2017). A unified framework, based on solute transport theory, helps predict soil depth as a function of age and infiltration rate (Yu and Hunt, 2017), soil erosion rates (Yu et al., 2019), chemical weathering (Yu and Hunt, 2018), and plant height and productivity as a function of time and transpiration rates (Hunt, 2017). Expressing soil depth and plant growth inputs to the crop net primary productivity, NPP, permits optimization of NPP with respect to the hydrologic fluxes (Hunt et al., 2020). Some remarkable conclusions also arise from this theory, such as that globally averaged ET is almost twice Q, and that the topology of the network guiding soil-water flow provides limitations on solute transport and chemical weathering. Both plant roots and infiltrating water tend to follow paths of least resistance, but with differing connectivity properties. Except in arid climates (Yang et al., 2016), roots tend to be restricted to the thin topsoil, so lateral root distributions are often considered two-dimensional (2D), and root structures employ hierarchical, directional organization, speeding transport by avoiding closed loops. In contrast, infiltrating water (i.e., the subsurface part of Q) tends to follow random paths (Hunt, 2017) and percolates through the topsoil more deeply, giving rise to three-dimensional (3D) flow-path structures. The resulting distinct topologies generate differing nonlinear scaling, which is fractal, between time and distance of solute transport.

On a bi-logarithmic space-time plot (Hunt, 2017), optimal paths for the different spatio-temporal scaling laws of root radial extent (RRE) and soil depth, z, are defined by their radial divergence from the same length and time positions. RRE relates to NPP, which is a key determinant of crop productivity, through root fractal dimensionality, d_f, given by RRE ∝ NPP^1/df, with predicted values of d_f of 1.9 and 2.5 for 2D and 3D patterns, respectively (Hunt and Sahimi, 2017). Basic length/time scales are given by the fundamental network size (determined from the soil particle size distribution) and its ratio to mean soil-water flow rate. Yearly average pore-scale flow rates are determined from climate variables (Yu and Hunt, 2017). Each scaling relationship has a spread, representing chiefly the range of flow rates as controlled by P and its partitioning into ET and Q. This conceptual basis makes possible prediction of the dependence of NPP on the hydrologic fluxes, Q (which modulates the soil and root depths), and evapotranspiration, given by ET = P − Q (which modulates RRE).

Consider the steady-state soil depth (Yu and Hunt, 2017), 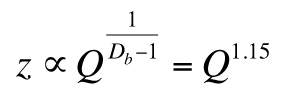with D_b = 1.87, governing solute transport, which is the backbone fractal dimension of percolation. Optimization of NPP ∝ RRE ∝ Q1.15(P − Q)^df with respect to Q by setting d(NPP) ⁄ d(Q) = 0 yields ET = P d_f ⁄(1.15 + d_f) = 0.623P, within 1–2% of the mean of global estimates (Hunt et al., 2020).

The ratio ET/P may be represented using the aridity index, AI, often defined as PET/P (sometimes as its inverse), with PET being the potential evapotranspiration (Budyko, 1958). In arid regions, where soil depths are yet increasing, 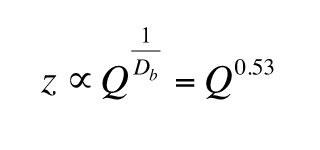(Yu and Hunt, 2017). For a bare land area, the fraction of the surface that plants occupy may be only P/PET, which is the inverse of the AI. Both tend to increase ET as a fraction of P. For high AI, roots are also less confined near the surface, searching water more deeply, and also increasing ET. Under ideal conditions of neither energy nor water limitation (AI = 1), Levang-Brilz and Biondini (2003) determined that for 16 grass and 39 Great Plains forb species the mean d_f for all forbs was 2.49, but grasses separated into two distinct groups with d_f = 2.65 and 1.67, in accord with percolation predictions (Hunt and Sahimi, 2017). In the studied biome, grasses constitute more than 90% of the biomass.

Figure 1 shows our predicted upper bound (dotted line) of ET/P as a function of AI. At low AI (<1) the known limit ET ≤ PET is applied. For large AI, d_f = 2.5, appropriate for deeper, more isotropic, root systems. Levang-Brilz and Biondini’s (2003) experimental d_f values generate the spread in predicted ET at selected AI values (though experimental values d_f > 3 that generate ET > P are not used). What is new is the representation of predicted variability in ET based on experimental d_f value at larger AI, not just AI = 1.

Values of d_f for grasses generate almost the exact observed variability in ET/P at AI = 1, but overestimate variability at larger AI. We attribute the discrepancy at larger AI mostly to the fact that low-end ET/P values come from grass species with d_f around 1.9, typical for nearly 2D structures, being less adapted to arid conditions, and more likely absent at larger AI. Our theoretical framework, together with experimentally determined parameters d_f, generates a good upper bound for ET/P from theory and its variability as a function of AI.

The most important theoretical limitations of applying percolation theory to water balance modeling arise from the partitioning of surface run-off and subsurface flow (and transpiration and interception), because these processes are not obviously regulated by plants for optimizing NPP. The ability to predict contributions of surface run-off, plant interception, and subsurface flow would also be important in evaluation of sequestering carbon and coupling global water and carbon cycles. Incorporating observations helps estimate these complementary fluxes. We found that variability in the predicted water balance due to variation in plant root fractal dimensionality outweighs uncertainties/variation in interception and surface run-off. Coupling our long-term percolation model with the short-term stochastic infiltration model (e.g., Rodriguez-Iturbe et al., 1999) might improve predictions of water balance components and optimization of plant productivity.

References Cited

1. Budyko, M.I., 1958, The heat balance of the earth’s surface: Washington, DC, U.S. Department of Commerce, Weather Bureau.
2. Gentine, P., D’Odorico, P., Linter, B.R., Sivandran, G., and Salvucci, G., 2012, Interdependence of climate, soil, and vegetation as constrained by the Budyko curve: Geophysical Research Letters, v. 39, L19404, https://doi.org/10.1029/2012GL053492.
3. Hunt, A.G., 2017, Spatio-temporal scaling of vegetation growth and soil formation: Explicit predictions: Vadose Zone Journal, https://doi.org/10.2136/vzj2016.06.0055.
4. Hunt, A.G., and Ghanbarian, B., 2016, Percolation theory for solute transport in porous media: Geochemistry, geomorphology, and carbon cycling: Water Resources Research, v. 52, p. 7444–7459, https://doi.org/10.1002/2016WR019289.
5. Hunt, A.G., and Sahimi, M., 2017, Flow, transport, and reaction in porous media: Percolation scaling, critical path analysis and effective medium approximation: Reviews of Geophysics, v. 55, p. 993–1078, https://doi.org/10.1002/2017RG000558.
6. Hunt, A.G., Faybishenko, B.A., Ghanbarian, B., Egli, M., and Yu, F., 2020, Predicting water cycle characteristics from percolation theory and observation: International Journal of Environmental Research and Public Health, v. 17, no. 3, p. 734, https://doi.org/10.3390/ijerph17030734.
7. Levang-Brilz, N., and Biondini, M.E., 2003, Growth rate, root development and nutrient uptake of 55 plant species from the Great Plains Grasslands, USA: Plant Ecology, v. 165, p. 117–144, https://doi.org/10.1023/A:1021469210691.
8. Rodriguez-Iturbe, I., Porporato, A., Ridolfi, L., Isham, V., and Cox, D.R., 1999, Probabilistic modelling of water balance at a point: The role of climate, soil and vegetation: Proceedings of the Royal Society of London, Series A, v. 455, p. 3789–3805, https://doi.org/10.1098/rspa.1999.0477.
9. Yang, Y., Donohue, R.J., and McVicar, T.R., 2016, Global estimation of effective plant rooting depth: Implications for hydrological modeling: Water Resources Research, v. 52, no. 10, https://doi.org/10.1002/2016WR019392.
10. Yu, F., and Hunt, A.G., 2017, Predicting soil formation on the basis of transport-limited chemical weathering: Geomorphology, https://doi.org/10.1016/j.geomorph.2017.10.027.
11. Yu, F., and Hunt, A.G., 2018, Damköhler number input to transport-limited chemical weathering calculations: ACS Earth & Space Chemistry, v. 1, p. 30–38, https://doi.org/10.1021/acsearthspacechem.6b00007.
12. Yu, F., Hunt, A.G., Egli, M., and Raab, G., 2019, Comparison and contrast in soil depth evolution for steady-state and stochastic erosion processes: Possible implications for landslide prediction: Geochemistry, Geophysics, Geosystems, v. 20, p. 2886–2906, https://doi.org/10.1029/2018GC008125.