Full Text View
Volume 20 Issue 3 (March 2010)
GSA Today
Article, pp. 4-10 | Abstract | PDF (2MB)
Evaluating lateral compaction in deepwater fold and thrust belts: How much are we missing from “nature’s sandbox”?
| Table of Contents |
|---|
|
Search GoogleScholar for
Search GSA Today |
Abstract
Deepwater fold and thrust belts offer unique opportunities for evaluating deformation in sedimentary successions with unrivalled seismic imaging of fold-thrust structures. A regional seismic line through the Orange Basin, offshore Namibia, reveals a classic paired, gravity-driven deformation system, over 100 km across, with extension high on the submarine slope and contraction toward the toe of slope. A mismatch between the minimum estimate of extension (44 km) and slip on thrusts (18–25 km) requires an additional longitudinal strain component of 18%–25% to be distributed across the system, most plausibly as lateral compaction and volume loss. Strains of this magnitude raise issues for understanding deformation in partially lithified strata, with implications for the applicability of theoretical fold-thrust models and the development of hydrocarbon resources in deepwater settings.
Manuscript received 17 August 2009; accepted 23 September 2009
DOI: 10.1130/GSATG77A.1
E-mail: ,
INTRODUCTION
The thick sedimentary sequences that characterize many of the world’s continental margins hold an unstable secret of gravitational collapse, the scale of which has only become apparent through exploration for hydrocarbons in the past 20 years or so (e.g., Rowan et al., 2004). Although inaccessible, submerged beneath many kilometers of water, these structures are revolutionizing the understanding of the geometry of contractional deformation in sedimentary successions. They are nature’s sandbox, large-scale versions of the laboratory physical models currently in vogue in some parts of the structural geology community (e.g., Adam et al., 2005). Here we examine one well-imaged system to learn more about the large-scale deformation of poorly lithified sedimentary rocks. Our case study comes from the continental margin of southwest Africa, offshore Namibia. By making independent estimates of the extension and the contraction, we show that there is a considerable amount of deformation that is not accounted for in the imaged thrust belt structures. We discuss how these inferred strains might be accommodated and outline the implications.
Deepwater fold and thrust belts are the down-slope expression of large-scale gravitational failure of submarine slopes (Rowan et al., 2004). They are paired with extensional structures higher on the slope (Fig. 1), with the two domains connected by a detachment preferentially located along a weak formation (salt, or, as in our study, over-pressured mudstone). There are two principal attractions for studying thrust systems created by gravity tectonics in deepwater systems. The first is that seismic reflection methods yield images of unrivalled clarity (Fig. 2). This means many of the ambiguities in structural interpretation are reduced, especially in defining stratal terminations against faults and thereby deducing the geometry and extent of thrust ramps and flats. Kinematic models that describe the relationship between folding, the geometry of stratal surfaces, and the displacement patterns on faults have been refined (e.g., Shaw et al., 2005) and reapplied (e.g., Briggs et al., 2006) in these settings. Second, purely gravity-driven systems are kinematically self-contained. The stratal shortening represented by the contractional structures, including the thrust and folds developed on the lower slopes, must balance the net extension accommodated higher on slopes. This attribute means estimates of the extensional motion can be used to constrain structural interpretations of the contractional domain. Our specific concern is whether the thrust and folds that can be interpreted from the seismic data are sufficient alone to balance the extension. If not, a further strain component is required, the value of which can be estimated. Distributed strains, long known as a component of foreland fold and thrust belts (e.g., Coward, 1988) and recently recognized in physical deformation models of granular aggregates in the laboratory (e.g., Adam et al., 2005), are commonly ignored in seismic interpretation and are not generally considered in theoretical fold-thrust models (e.g., Shaw et al., 2005). Estimating the significance of distributed strains on a large scale, and how they might be accommodated, is important for the general understanding of deformation in sedimentary successions, especially those that are only partly lithified. Such deformation can also impact petrophysical properties, especially the performance of hydrocarbon reservoirs (e.g., Zahid and Uddin, 2005).
|
Architecture of gravity-driven thrust systems, based on the Pará-Maranhão basin, offshore Brazil (Zalan, 2005). The pre-kinematic section is shown in green and has been stacked up into a deepwater thrust belt on the lower slope. Sedimentation has continued (tan-yellow tones) and eventually buried the thrust belt. These syn-kinematic deposits are ponded in fault-related basins within the extensional domain, upslope from the thrust belt. The sediments show characteristic geometry of growth strata, thickening toward the main extensional faults and forming off-lapping depositional wedges that become progressively younger up the slope. Cumulative stratal shortening in the contractional domain should balance the net extension, here shown by the separation of pre-kinematic strata along the main detachment. |
|
High-quality seismic reflection data reveal thrust and fold structural geometry offshore Namibia. The context is provided on Fig. 3; these are the lowest structures on the slope (thrusts 1–6 on Fig. 5A). This image is ~17 km across and 2.5 s (seismic two-way-time) high, which equates to an approximate vertical exaggeration of 5:1 assuming a constant seismic velocity of 2.7 km/s. Image courtesy CGGVeritas and the Virtual Seismic Atlas. |
GEOLOGICAL SETTING AND REGIONAL STRUCTURE
The regional seismic line used in this study comes from the multi-client 2-D survey VERNOB03 acquired by CGGVeritas in 2003, offshore Namibia. The line is 215 km long and was originally recorded to 8 seconds. The acquisition streamer was 8 km long, with 320 receivers. The seismic profile was processed using modern Kirchhoff pre-stack migration that yields excellent reflector continuity, notwithstanding the structural complexity. The lack of image distortion and amplitude variations associated with structures indicates a simple seismic velocity structure that is a function of depth rather than stratigraphy. The profiles are shown here in seismic two-way-time. The measurements of bed-length and separations across faults are dominantly subhorizontal, so velocity variations are not considered to impact these significantly. Depth comparisons are provided in figure captions. The seismic line (Fig. 3) runs down in the dip direction of the continental margin and shows a prominent paired system of extension and contraction bounded top and bottom by undeformed strata. The images shown here are available via the Virtual Seismic Atlas (www.seismicatlas.org) so that readers can inspect the seismic line with and without interpretation.
|
Regional seismic reflection profile across the continental margin offshore Namibia (see inset) shown in clean and interpreted form. Assuming a mean seismic velocity of 2.7 km/s, the vertical exaggeration is ~7:1. Original image courtesy of CGGVeritas and the Virtual Seismic Atlas. |
The regional setting and tectonostratigraphic evolution of the margin, termed the Orange Basin, are described by Paton et al. (2008) and de Vera et al. (2009). Our study is concerned with deformation in part of the post-rift section. Although there is no well control on the line of section, the stratigraphy on the shelf can be tied regionally to wells on the shelf. Continental rifting in the Late Jurassic and Early Cretaceous led to continental breakup in the Barremian. Once established as a continental margin, a wedge of sediment built out (in places >5.5 km thick), sourced principally from the ancestral Orange River. Paton et al. (2008) note that this post-rift megasequence developed in two distinct phases, separated by a tilting episode that correlates with the deformation studied here. The regional detachment, together with the underlying strata, dips consistently toward the ocean. Thus, the deformation approximates to gravity sliding (Rowan et al., 2004).
Structural interpretation
The general form of the gravitational deformation system is shown on Figure 3. The extensional domain is 80 km across, while the thrust belt is 55 km wide. The two domains are separated by a 10-km-wide zone where the seismic imaging and hence structural style is ambiguous. It is possible that this represents a transitional domain of polyphase deformation involving extension overprinting thrusting (de Vera et al., 2009), as found in other systems worldwide (e.g., Rowan et al., 2004). In the following discussion, the lack of clearly decipherable structures in this domain represents an interpretational uncertainty but this is considered here to be minor.
Beneath the main system interpreted on Figure 3 is a local patch of deformation, 20 km across. This is a small, paired extensional-contractional system, most likely formed toward the end of the translation on the main detachment above, which is broadly folded by it. The thrust ramp is essentially unmoved, with the anticline in its hanging wall remaining above the footwall ramp. Therefore, although the width of the structure and the structural relief created by it are significant, the amount of down-slope translation accommodated is likely to be rather small (<1 km). It is not considered further.
The structural geometry evident on the interpreted seismic section can be used to estimate the displacements, both in the extensional and in the contractional domain. As Bond et al. (2007) point out, geological interpretations are fundamentally non-unique. Therefore, we spend some time discussing interpretations and limitations. The two deformation domains (extensional and contractional) are considered independently, and the linear values for the two are compared to assess any shortfall in the required deformation. The analysis carries the tacit assumptions of plane strain and that there are no significant dips out of the plane, both of which are reasonable because the profile is perpendicular to regional slope.
The Extensional Domain
Figure 4 shows the extensional part of the system. Strata above the detachment are characterized by convex-upward geometries that diverge downward, increasing in dip as they do so, terminating against the system detachment. This pattern is diagnostic of growth strata in extensional systems (Williams, 1993; cf. Fig. 1). Up-dip, the growth strata are separated by normal faults (at B and C on Fig. 4B) from subhorizontal reflectors of the undeformed African shelf. Down-dip, the growth strata abut onto the transitional domain at the trailing edge of the thrust belt (A on Fig. 4B).
|
A structural interpretation of the extensional domain, offshore Namibia, as located on Fig. 3. A. Clean line (courtesy of CGGVeritas and the Virtual Seismic Atlas). B. Interpreted section showing arbitrarily selected correlations across faults and wedges of growth strata (green and blue tones). The base of the growth strata is outlined by the thick blue pick; regional detachment and faults are in red. These sections have a vertical exaggeration of ~ 3.75:1, assuming a constant velocity of 2.7 km/s. C. The same structure with little inferred vertical exaggeration. The maximum extension implied by the separation along the detachment (distance from A–C) is 71 km, reducing to 44 km if the residual pre-kinematic strata is included. See text for further discussion. |
Evaluating the extent of growth strata in the extensional domain is important. If the entire stratal volume above the detachment is synkinematic, then the separation between the trailing edge of the thrust belt and the undeformed shelf, as shown on Figure 1, provides an estimate of the amount of extension. On Figure 4, this is the distance between points A and B, which is measured at 67 km. Note that if the trailing edge of the thrust belt (A) lies at the top of the stratal package, it would match with a higher position along the detachment (i.e., C on Fig. 4). Such an interpretation increases the total separation along the detachment to 71 km, a figure that can be considered to represent a maximum plausible estimate of the extension implied by this geological interpretation.
If 71 km represents the maximum value for extension, lower values are obtained if part of the rock volume in the hanging wall to the detachment is represented by pre- rather than wholly syn-kinematic strata. Such uncertainty exists within the geological interpretation because stratal geometries approaching the detachment are obscure. If these ambiguous portions are pre-kinematic, then the additional length of the top of these strata must be subtracted from the total separation value obtained. A conservative interpretation is shown on Fig. 4B, with the picked horizon at the top of possible pre-kinematic strata having an integrated restored length of 23 km. Thus, a conservative value for extensional movement on the detachment is 67 − 23 = 44 km.
Structure of the Thrust Belt
Section balancing has long been a mainstay of structural interpretation in thrust belts. Conventionally, when generating a structural interpretation, mismatches in bed-length are resolved to create a balanced cross section. The final version will be the result of considerable iteration and compromise, trading off lengths of beds, resolving thrust trajectories to create a coherent geometric model of the present-day structure. The result may be used to estimate the large-scale shortening accommodated by the structures shown on the cross section, simply by subtracting the length of the final state section from that of its restored counterpart. An unusual strategy is adopted here, showing a cross section that does not balance in its entirety. By showing this “provisional” unbalanced cross section, we reveal interpretation uncertainties that would otherwise become iterated away, potentially implying unwarranted precision in the values for stratal contraction so obtained.
The thrust belt is here restored using two seismic-stratigraphic markers that can be correlated through the system and into the undeformed strata lying farther out on the abyssal plain. For the outer thrust system (thrusts 1–13, Fig. 5), the lengths of these two horizons restore to comparable lengths. The position of thrust ramps through the strata can be estimated with confidence given the clear imaging of matching hanging-wall and footwall stratal cut-offs. Deformation in these outer thrust slices appears therefore to be accommodated by thrust displacement and the associated folding of stratal layers. There is no difference between the restored lengths of the two marker horizons, indicating that there is no distributed strain accumulated heterogeneously in the section. Furthermore, the thickness of the two stratal layers and the intervening units is conserved from the undeformed section into and between the thrust slices. Thus, there is no evidence in these outer structures for distributed vertical stretching (layer parallel shortening). Consequently, the assumption of bed-length conservation inherent in the restoration appears valid.
|
Structural interpretation of the thrust belt (A), offshore Namibia, and restoration (B) used to estimate the amount of stratal shortening represented in the contractional domain. The section is shown with no significant vertical exaggeration (assuming a seismic velocity of 2.7 km/s). Thrusts are numbered for reference and do not imply a sequence of formation. The deformed distance between the pin line and trail line 2A (blue horizon) is 58.5 km; its restored equivalent distance is 77 km, so the net contraction is 18.5 km. The deformed distance between the pin line and trail line 2B (green horizon) is 60 km; its restored equivalent is 85 km, so the net contraction is 25 km. |
In detail, the contractional structures upslope behind the lower thrust belt (14–29 on Fig. 5) become increasingly ambiguous. Although the two marker horizons can be traced confidently across the thrust belt, more problematic geometries arise from uncertainty in picking thrust cut-offs. Initially, this is manifest in a first-pass restoration as a cumulative mismatch on the restored section between the ramps cutting the two marker horizons (thrusts >23 on Fig. 5). The most upslope thrust slices (>29 on Fig. 5) are increasingly difficult to balance. Their seismic stratigraphy is harder to correlate across faults because the distinctiveness of the marker horizons is diminished. A number of different structural geometries satisfy the available data, and there may be further structures hindward of fault 32. The option chosen in Figure 5 is extreme, maximizing the amount of stratal length of the lower marker horizon. While creating a significant mismatch in the restored lengths of the two horizons, it inflates the required shortening value for the thrust belt as a whole. Comparing the shortening on the two marker beds therefore gives an estimate of uncertainty in the net contraction in the thrust belt. On Figure 5, the upper (blue) horizon shows 18.5 km shortening, while the lower (green) level shows 25 km. This difference might be explained by further shortening (concentrated in the blue marker horizon) in the poorly imaged zone of transition into the extensional domain, although this suggestion is speculative and unquantifiable.
Matching Displacements: Comparison between the Extensional and Contractional Domains
It is evident that the net contraction on folds and thrusts interpreted on Figure 5 (18.5 km–25 km) cannot accommodate the value required to balance even the minimum estimate of extension (44 km). We have not considered the structure of the poorly imaged transitional domain between the extensional and contractional structures, and therefore this represents an unquantified uncertainty in our analysis. However, if de Vera et al. (2009) are correct that extension and contraction are present in the transitional domain, the net effect is likely to be small. These authors also report a mismatch between extension and contraction on the whole section line. While their estimate of shortening in the thrust belt is broadly comparable with our minimum estimate (16 km vs. 18.5 km), we consider their value of extension (24 km) to be an underestimate caused by assuming excessive amounts of pre-kinematic strata within the extensional domain. The shortfall in required stratal shortening in both studies demands another strain component to be present and implies that our routine restoration of stratal lengths is insufficient.
VOLUME LOSS AND LATERAL COMPACTION
On occasion, the presence of distributed strain to achieve a balance in deformed multilayers (e.g., Butler, 1992) has been inferred and ductile layer parallel shortening measured (e.g., Coward, 1988) in some foreland fold and thrust belts. These examples have focused on well-lithified strata. However, where lithification is incomplete, contractional deformation can include volume loss. Henry et al. (2003) estimate 12% horizontal ductile shortening based on core samples from the Nankai subduction-accretion thrust system. Synkinematic fluid expulsion, and therefore volume loss, is evident in submarine thrust belts, especially where it is focused, for example, at mud volcanoes (e.g., Kopf et al., 2001). Recently, models of fold-thrust development have been modified to include strain and volume loss (e.g., Gonzalez-Mieres and Suppe, 2006). Our study of the Namibia deepwater fold and thrust belt offers an opportunity to quantify these effects on a regional scale.
Table 1 |
If the stratal contraction in our Namibian study cannot be accounted for in full, the shortfall is presumably taken up as widely distributed ductile deformation (Fig. 6), as calculated in Table 1. This equates to 18%–25% longitudinal strain (or lateral volume loss) if distributed homogeneously through the entire contractional domain. This deformation presumably predated the localization of thrusts (Fig. 6), because thrust trajectories and bed dips, certainly for the well-imaged frontal part of the contractional domain (thrusts 1–12 on Fig. 5), appear unmodified by subsequent deformation. The seismic data show no evidence for minor faulting in picked horizons (e.g., Fig. 2) or for significant bed-thickness variations between the undeformed basin floor and thrust belt. Thus, the likely deformation mechanism accommodating this missing strain was distributed volume loss. Presumably, this strain was homogeneously developed with depth for the frontal thrusts (thrusts 1–12 balance the green and blue markers on Fig. 5). Heterogeneous lateral compaction (stronger in the blue horizon) may explain the mismatch between the restoration of markers toward the back of the contractional domain.
|
A conceptual model for gravitational tectonics on continental margins, where the down-dip translation associated with extension higher on the slope passes into a zone where contraction is accommodated by lateral compaction and volume loss. It is possible that in some situations the contractional deformation happens without any observable thrusting or folding. |
DISCUSSION
Our structural interpretation and restoration of the deepwater fold and thrust belt offshore Namibia indicates that a significant proportion of the slip required to balance the extensional displacements higher on the slope must be accommodated by widely distributed ductile deformation, most plausibly lateral compaction and volume loss (Fig. 6). The required values of 18%–25% volume loss are significant. We hope our investigation prompts further studies elsewhere to establish how deformation is partitioned between localized thrusting, ductile deformation, and lateral compaction, especially within poorly lithified sedimentary successions. Not only do these include other gravity-driven thrust belts but also accretionary prisms and parts of weakly buried foreland thrust belts. Our conclusions raise issues for structural analysis in these settings.
Lateral compaction renders the assumption of bed-length conservation, implicit in most theoretical descriptions of fold-thrust relationships (e.g., Shaw et al., 2005), invalid. A greater range of structural geometries exists with the additional freedom of significant distributed strain (e.g., Gonzalez-Mieres and Suppe, 2006). In hydrocarbon exploration, the application of the established fold-thrust models has led to over-optimistic predictions of structural integrity and, hence, oil column heights (e.g., Kostenko et al., 2008). Penetrative layer-parallel shortening and lateral compaction can lead to significant anisotropy in the poro-perm characteristics of reservoirs (e.g., Henry et al., 2003), which will have an impact during production. It is tempting to believe that when seismic imaging is as excellent as in deepwater thrust belts (e.g., Fig. 2) we can recognize all the deformation. Three-dimensional data can help to resolve smaller structures and distributed strains predicted here (e.g., Bangs and Gulick, 2005), perhaps using regional maps of seismic amplitude anomalies. The challenge lies in placing these detailed studies in their regional context so models of the kinematic evolution of the contractional domains can be tested against the deformation requirements of the whole gravitational system.
ACKNOWLEDGMENTS
The images used for this paper were released to the Virtual Seismic Atlas (VSA) by CGGVeritas (formerly Veritas DGC), which is gratefully acknowledged. All images used here are available for inspection and re-interpretation on the VSA at www.seismicatlas.org. In addition, we thank R. Morgan and W.D. McCaffrey for discussions on deepwater systems, together with two anonymous referees and editor Stephen Johnston for helpful comments on an earlier draft. Our work on submarine thrust belts was supported by BHP-Billiton.
REFERENCES CITED
- Adam, J., Urai, J.L., Wieneke, B., Oncken, O., Pfeiffer, K., Kukowski, N., Lohrman, J., Hoth, S., van der Zee, W., and Schmatz, J., 2005, Shear localization and strain distribution during tectonic faulting—New insights from granular-flow experiments and high-resolution optical image correlation techniques: Journal of Structural Geology, v. 27, p. 283–301.
- Bangs, N.L.B., and Gulick, S.P.S., 2005, Physical properties along the developing décollement in the Nankai Trough: Inferences from 3-D seismic reflection data inversion and Leg 190 and 196 drilling data, in Mikada, H., Morre, G.F., Taira, A., Becker, K., Moore, J.C., and Laus, A., eds, Proceedings of Ocean Drilling Program Legs 190/196, Scientific Results, p. 1–18.
- Bond, C.E., Gibbs, A.D., Shipton, Z.K., and Jones, S., 2007, What do you think this is? “Conceptual uncertainty” in geoscience interpretation: GSA Today, v. 17, no. 11, p. 4–10.
- Briggs, S., Davies, R.J., Cartwright, J.A., and Morgan, R., 2006, Multiple detachment levels and their control on fold styles in the compressional domain of the deepwater west Niger Delta: Basin Research, v. 18, p. 435–450.
- Butler, R.W.H., 1992, Structural evolution of the western Chartreuse fold-thrust system, NW French Subalpine chains, in McClay, K.R., ed., Thrust Tectonics: London, Chapman & Hall, p. 287–298.
- Coward, M.P., 1988, The Moine thrust and the Scottish Caledonides, in Mitra, G., and Wojtal, S., eds, Geometries and mechanisms of thrusting with special reference to the Appalachians: GSA Special Paper 222, p. 1–16.
- de Vera, J., Granado, P., and McClay, K.R., 2009, Structural evolution of the Orange Basin gravity-driven system, offshore Namibia: Marine and Petroleum Geology, v. 27, p. 223–237.
- Gonzalez-Mieres, R., and Suppe, J., 2006, Relief and shortening in detachment folds: Journal of Structural Geology, v. 28, p. 1785–1807.
- Henry, P., Jouniaux, L., Screaton, E.J., Hunze, S., and Saffer, D.M., 2003, Anisotropy of electrical conductivity record of initial strain at the toe of the Nankai accretionary prism: Journal of Geophysical Research, v. 108, doi: 10.1029/2002JB002287.
- Kopf, A., Klaeschen, D., and Mascle, J., 2001, Extreme efficiency of mud volcanism in dewatering accretionary prisms: Earth and Planetary Science Letters, v. 189, p. 295–313.
- Kostenko, O.V., Naruk, S.J., Hack, W., Poupon, M., Meyer, H-J., Mora-Glukstad, M., Anowai, C., and Mordi, M., 2008, Structural evaluation of column-height controls at a toe-thrust discovery, deep-water Niger Delta: AAPG Bulletin, v. 92, p. 1615–1638.
- Paton, D.A., van der Spuy, D., di Primio, R., and Horsfield, B., 2008, Tectonically induced adjustment of passive-margin accommodation space; influence on hydrocarbon potential of the Orange Basin, South Africa: AAPG Bulletin, v. 92, p. 589–609.
- Rowan, M.G., Peel, F.J., and Vendeville, B.C., 2004, Gravity-driven fold belts on passive margins, in McClay, K.R., ed., Thrust tectonics and hydrocarbon systems: AAPG Memoir 82, p. 157–182.
- Shaw, J.H., Connors, C., and Suppe, J., eds., 2005, Seismic interpretation of contractional fault-related folds: An AAPG Seismic Atlas: AAPG Studies in Geology 53, p. 156.
- Virtual Seismic Atlas, 2008: SeismicAtlas.org, University of Aberdeen and University of Leeds, http://www.seismicatlas.org (last accessed 11 Jan. 2010).
- Williams, G.D., 1993, Tectonics and seismic sequence stratigraphy: An introduction, in Williams, G.D., and Dobb, A., eds., Tectonics and seismic sequence stratigraphy: London, Geological Society Special Publication 71, p. 1–14.
- Zahid, K.M., and Uddin, A., 2005, Influence of overpressure on formation velocity evaluation of Neogene strata from the eastern Bengal Basin, Bangladesh: Journal of Asian Earth Sciences, v. 25, p. 419–429.
- Zalan, P.V., 2005, End members of gravitational fold and thrust belts (GFTBs) in the deep waters of Brazil, in Shaw, J.H., Connors, C., and Suppe, J., eds., An AAPG Seismic Atlas: AAPG Studies in Geology 53, p. 147–156.

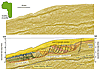 Figure 3
Figure 3 Figure 4
Figure 4